Every once in a while in woodworking, we run into the need to create a precise ellipse, or we need an ellipse which is just too large for standard jigs. While there are many methods and jigs for creating ovals, creating a true mathematical ellipse with any degree of precision is not as simple. The string method is based on the mathematical definition of an ellipse.

I am sure you are thinking, "why would I ever need a precise ellipse?" Let's take an example that I ran into recently. I was contracted to build a fireplace surround which had an elliptical fascia. To conform to the interior tile work, the ellipse had to be precisely 52 inches wide, and 12 inches tall. I could not vary from these dimensions by more than 1/8 of an inch, or it would have impacted other architectural components in the room.

To draw an ellipse with this precision, all I needed was a piece of string, two nails, and a pencil. Where to place the nails, and how long the string should be are determined by the parameters of your ellipse.

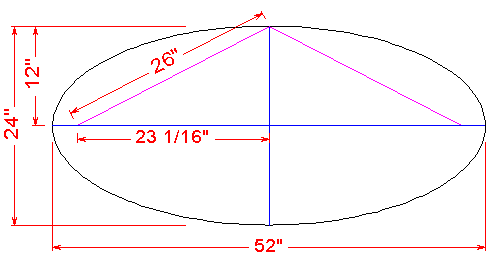
To begin, draw a horizontal line whose length is the same as your ellipse's width. In my example, this is 52 inches long. Next, from the center of this line, draw a vertical line whose length is the same as your ellipse's height. In my case, this line extends 12 inches above and below the first line. (These two lines are shown in blue in the drawing above.)

Next, you will need the string. For best results, this should be a type of string which does not stretch, or it could even be a braided wire used for hanging pictures. Take this string and tie loops in each end, such that the total length of the string is the same as the width of your ellipse (52 inches for this example). {Hint: It may be easier to pound two nails into a board 52 inches apart, and use these to help you tie the loops at the correct distance.)

The next step is to locate where the nails go. Even though there is an equation for this, there is a very simple method which uses the string. Fold the string in half so that it is 26 inches long for this example, and place one end at the top of the ellipse. Place the nails at the intersection of the string, and the horizontal line you drew earlier. (The string is shown in purple in the drawing above.) {By the way, if you used the Pythagorean theorem, you could have calculated the distance of 23 1/16 inches as shown in the drawing.}

That's it. Now we can draw our ellipse. Take the string, and place a loop over each of the nails. Using the string to control the path of the pencil, trace out the ellipse. With a little bit of creativity, you could even set up a router jig, where the router would follow the string, although, make sure that there is no chance for the string to get caught up in the spinning router bit.