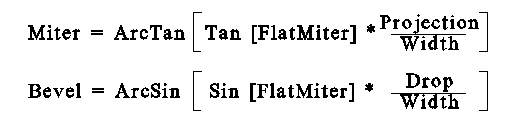Compound Miter Settings

Compound Angles
By Rick Christopherson

Update: This article was originally written in 1998. I have wanted to rewrite this article for many years with better graphics and an online calculator. When Festool-USA asked me to write the owner's manual for their (then) new Kapex mitersaw in 2009, I finally had the opportunity to rework this information. However, it was formatted for PDF output, not HTML. So I did not want to completely replace this HTML version with a straight link to the PDF. The information between the two is the same, but the PDF version may use different variable names, and includes more information than this HTML version. It also includes additional information regarding cutting crown moulding using standard miter techniques as well as compound miter techniques. It also explains how to apply this information to other applications beyond simple crown moulding.

I recommend reading the PDF instead of this HTML version. If your internet browser is setup to view PDFs directly in the browser and the calculator doesn't work for you, then right-click on the link below and save the file on your computer. Some people have reported that the calculator does not work on their computer, but I have not had enough comments to determine under what conditions this may be happening.

This Compound Miter (PDF) document is the 3 pages extracted directly from the Festool Kapex manual. Even if you don't own a Festool Kapex mitersaw, you may still want to read the entire Kapex Supplemental Owner's Manual because it contains additional information that can be applied to your brand of miter saw, such as calibrating the miter settings using the 4-cut calibration method, and includes a built-in calculator for that as well.

While there are several different methods for cutting mouldings, sometimes the best method is to use compound angle settings on a miter saw, radial arm saw, or a table saw. This isn't necessarily limited to cutting mouldings though. There are many other applications where compound miter settings are needed, like the roof of a doll house for example. Below is a set of equations for determining the compound angle settings for your miter saw. These equations will work for any compound angle, but I use crown moulding around a ceiling as my example, since this is easy to visualize.

In their original form, the equations are very simple and only use two variables. To make the equations easier to use in the shop, I have rearranged the equations in two different forms. These are all the same equations, but they are just mathematically manipulated to help you out. Which equation best suits your needs will depend on how fluent you are in mathematics, and what variables are known when you start. (I have also compiled a quick reference page to keep in your shop. This is just a duplication of the graphic images shown below.)

Getting Started
As I stated, there are only two variables needed to use these equations. The first variable deals with the angle of the room, picture frame, roof, or how many sides a box has. I have setup my equations in such a way that it doesn't matter whether you are making an inside corner or an outside corner. This is where many woodworkers make mistakes because we are not accustomed to working with numbers greater than 90°. For example, if you were placing crown moulding around the top of a square column, other equations would require you to use the "true" angle of 270°, and if you didn't, the results would be abnormal miter settings. The equations I derived use the angles the way a woodworker sees them, not a mathematician.

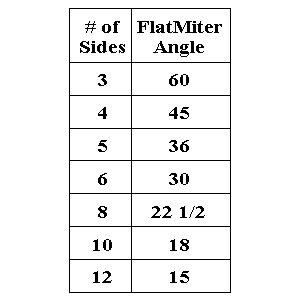FlatMiter
I will call this first variable the FlatMiter (1/2 the "Corner Angle" used in the PDF version). This variable is the angle which you would normally set your saw to, in order to miter a piece of flat moulding. In other words, if you were putting crown moulding up around a square room, the FlatMiter would be 45°. The table to the right shows the FlatMiter values based on how many sides a room or box has.

If your application doesn't fit into the category of being able to count the number of sides a box has, you can simply calculate the FlatMiter variable. Let's say you measured the corner of a box and found it to be 94° instead of the normal 90°. Then your FlatMiter variable would be 47°, which is ½ of 94 °.

Remember, with the exception of a triangular frame or the example above, your FlatMiter variable should always be less than 45°.

Slope
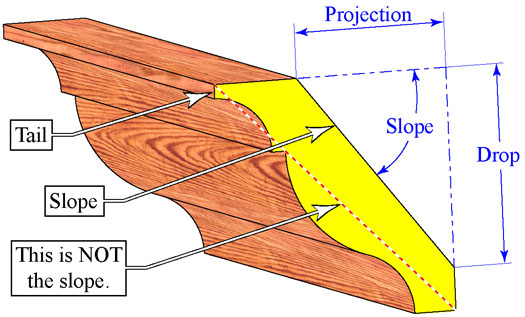(new graphic added from PDF) The second variable deals with the slope of the moulding or the pitch of a roof. Most crown mouldings do not rest against the wall at 45°. As a matter of fact, there is no set slope for crown mouldings. While a 38/52 moulding may be common, it is not exclusive. The slope of the moulding is dependent on the manufacturer and their machine settings.

While you may know the slope when dealing with a doll house roof, chances are, you won't know the slope of a specific crown moulding. Because of this I have rearranged the equations so that you can use Drop-Projection-Width, or just the slope. (Important Note: Notice that when measuring these variables, they are measured with respect to the flat side on the back of the moulding. This is because the flat side is the surface you place against the saw's table when you cut it. If you measure from the face of the moulding, the slope of the moulding will be wrong.) Since the Drop-Projection-Width equation is probably the most useful, I will start with that one.

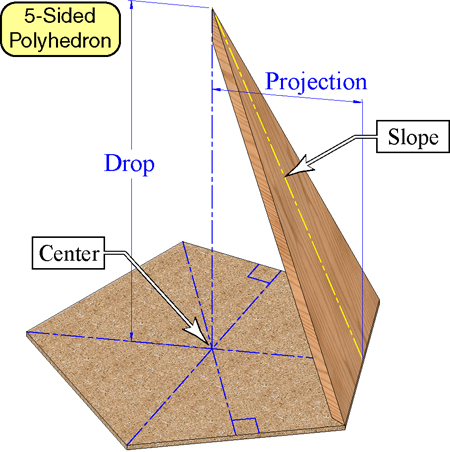
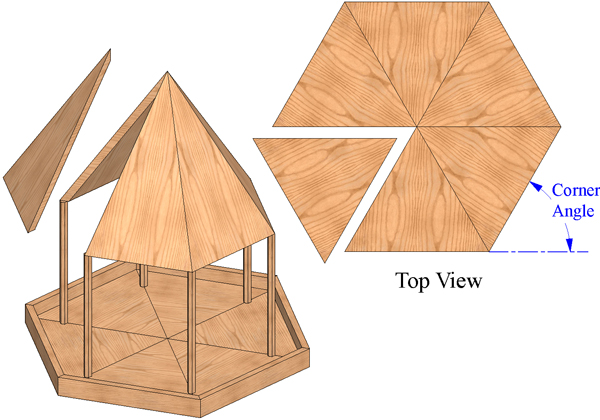
A couple new graphics from the PDF version:
The "Corner Angle" in the second graphic is a better way of describing the method for finding the "Flat Miter" in this original HTML article. The FlatMiter is 1/2 of the Corner Angle. The Corner Angle is 360 divided by the number sides, and the Flat Miter is 1/2 of that.

Drop-Projection-Width
If you feel more comfortable holding a tape measure than you do with a calculator, then this method is the best. Using a framing square, measure the Drop, Projection and Width as shown in the above drawing. Then apply this into the following Equations:

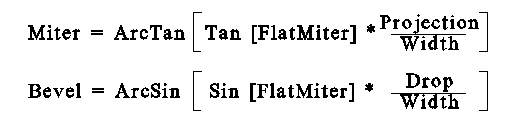
Slope
If you are familiar with geometry, you may recognize the "Drop/Width" as the Sine of an angle, and the "Projection/Width" as the Cosine of an angle. Just by replacing this information into the above equations, we end up with the following:

Unless you are building a three sided box, your miter and bevel settings should never be greater than 45°. Furthermore, the calculated compound miter angle should never be equal to or larger than a flat miter setting.

As I said earlier, these equations can be used for more than just mouldings. I have used them for many different applications when I needed a compound angle. The key to this is to visuallize what your setup would be like if it was a simple moulding. In otherwords, picture your application as though it was a moulding placed in the corner of a room up at the ceiling.

If you found this article from a search engine, and would like to
jump to the Waterfront Woods Home page, click on the image below.

Email Rick Christopherson